哈希冲突
哈希冲突
线性寻址
Cuckoo Hashing
最初的布谷鸟哈希使用了 hash1() 和 hash2() 两个哈希函数以及 T1、T2 两个表来存放键值对。它保证大多数键值对能在 T1 或 T2 中的一次哈希中就被找到(O(1)),这要优于某种情况下需要连续查找十几个位置的线性寻址方法。不过其弱势也很明显,其插入非常消耗性能,因为要对入口进行重排。如果 hash1(x) 在 T1 和 hash2(x) 在 T2 的位置都被占了,那么选择其中一个表中的元素如 T1 中的 y,用 x 把 y 的位置占了(鸠占鹊巢),然后继续计算 hash2(y) 在 T2 的位置。如果此时又遇到了碰撞,则继续递归地计算鸠占鹊巢(用 y 占新元素然后再找新元素的位置)。当然,如果计算了一堆位置仍然有碰撞存在,那只能选择给桶扩容了。一般情况下,会在负载因子大于 0.5 时主动扩容。而多个表带来了另外一个问题,布谷鸟哈希需要在多个位置寻找元素,这这些位置并不是临近的。在硬件上,其读取速度取决于硬盘随机读取速度。
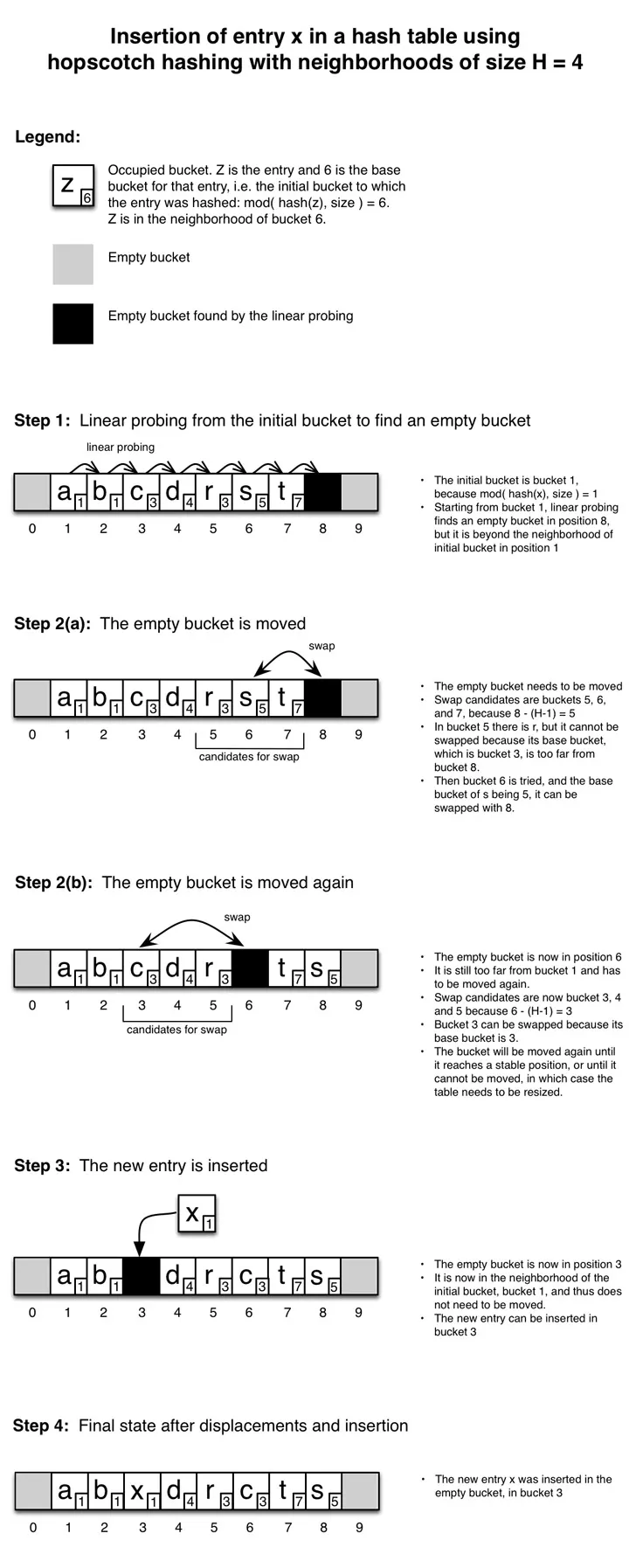
Hopscotch hashing
跳房子哈希规定每一个桶都拥有其在储存顺序中接下来 H 个位置的邻域,当出现碰撞时,值会储存到桶或其邻域中,这保证了常数级的读取时间,且相比布谷鸟哈希提高了缓存利用率。
在给新元素寻找空位时,使用线性寻址。如果找到的这个空位的地址不在初始位置或其邻域中,那么回溯 H 个地址并逐个检查这些地址能否于空位进行交换。如果不会把值抛出其对应的邻域,就能交换,这样一来空位就离其初始地址要近一些。一直交换,直到能把新元素储存到其初始位置的邻域中。
Robin Hood hashing
罗宾汉哈希记录下每一个元素其储存位置与初始位置的偏移量 DIB,并在插入新元素时对比这些偏移量。它使用线性寻址逐个对比当前位置与新元素的 DIB,并把 DIB 更大的那个储存当前位置,然后继续扫描,直到放下所有元素。这种算法会使得所有元素距离的 DIB 的方差较小,让读取时间解决常数级。

判断元素是否在表中的算法会比其它哈希稍微繁琐一些,因为它使用线性扫描会得到四种情况:找到该元素、找到空桶、找到某扫描元素其 DIB 小于当前扫描距离、找到某扫描元素其 DIB 大于等于当前扫描距离。其中,找到某不等于该元素的元素,如果其 DIB 大于等于当前扫描距离,则需要继续线性扫描,直到遇见剩下三种情况才能分辨该元素是否位于表中,停止扫描。
为了使删除元素不需要像插入元素那样交换入口的位置,一般会给删除的对象打一个墓碑标记,以在后续插入时将它当作一个空元素。Emmanuel 还介绍了一种性能更好的删除方法,向后移位法,见原文引用。